
背景をぼかして被写体を浮き上がらせるのは構図作りの定番テクニックです。このボケを出すには、明るい(F値の小さい)レンズか、望遠レンズを使います。もっと一般的な言い方をすれば、ボケの量には以下の法則があります。
- レンズは明るい(F値が小さい)ほど、大きくボケる
- 焦点距離は大きいほど、大きくボケる
- カメラと被写体との距離は近いほど、大きくボケる(被写体と背景の距離が変わらないとして)
では、望遠レンズ(焦点距離の大きいレンズ)と広角レンズ(焦点距離の小さいレンズ)のどちらが大きくボケるでしょう?これは意外に難しい問いです。望遠レンズを使うときは、広角レンズを使うときよりも被写体から離れて撮影する場合が多いため、
- 焦点距離で考えれば、望遠レンズの方が大きくボケそう
- でも、カメラと被写体との距離で考えれば、広角レンズの方が大きくボケそう
このように焦点距離の効果と、カメラと被写体との距離の効果が逆になります。ですから、直感ではどちらが大きくボケるか答えることはできません。
実際、下の掲示板のように望遠レンズと広角レンズのどちらが大きくボケるか、議論になっても答えを出せないことが多いようです。
この記事では、被写体が同じ大きさに写るようにカメラと被写体の距離を調節する場合、望遠レンズは広角レンズよりも背景が大きくボケることを数値的に示します。
まずは撮影条件の整理
ボケの量を比較するにあたって、撮影条件をはっきりさせておきます。
カメラと被写体の距離が同じで、レンズの焦点距離を変えると写る大きさが変わってしまいます。そこで、レンズの焦点距離に応じて、カメラと被写体の距離を調整して、被写体の写る大きさを一定にすることにします
被写体距離(カメラと被写体の距離)をs, 背景距離(被写体と背景の距離)をDfとします。
焦点距離fに応じて被写体距離を調整して同じ大きさで被写体が写るようにするには、被写体距離s÷焦点距離fが一定になるようにする必要があります(詳しい説明は,以下の記事を見てください)。つまり、焦点距離fが倍のレンズを使うなら、被写体距離sを倍にすれば同じ大きさで被写体が写ります。
焦点距離とボケ量の関係
ボケの大きさについて考えてみましょう。ピントが合っているとき、被写体のある1点から出た光は、レンズによって撮像素子上の1点に集まります。ピントが合っていないと、撮像素子上では点ではなくてにじんだ円になります。このにじんだ円の大きさをボケの大きさと呼ぶことにします。詳しくは別エントリ「カメラの用語(焦点距離・ボケ・被写界深度・過焦点距離等)を徹底解説、ただし長いです。」を見てください。
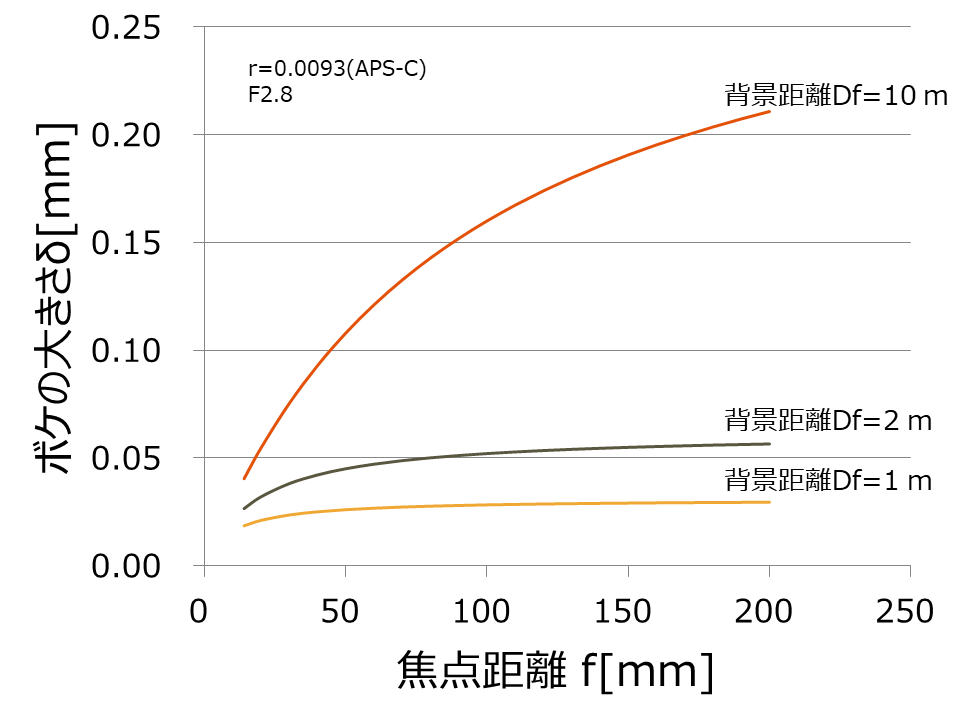
背景距離Df(被写体と背景の距離)を10m,2m,1mの3つの場合で、焦点距離とボケの大きさをグラフにしました(計算方法は文末の計算式を見てください)。ここでボケの大きさは、背景のボケの大きさです(つまり、被写体にピントを合わせた場合に背景距離Dfに置いた物から出た光が撮像素子上でにじむ円の大きさ)。
下のグラフから、望遠レンズ(焦点距離が長いほど)はよくボケることが分かります。特に被写体と背景との距離が広いときは、焦点距離が長いほど良くボケます。
被写界深度とボケ量の不思議な関係
ネットの情報を見てみると、ボケの大きさと被写界深度を区別していない記事を多く見ますが、これを区別することは大切です。この記事ではボケの大きさで説明してきました。一方、望遠レンズと広角レンズで被写界深度がどの程度変わるかについては別エントリで書いておきました。
「被写界深度の不思議、望遠レンズでも被写界深度は変わらない 」
被写界深度は望遠レンズでも広角レンズとほとんど変わりません。それなのにボケ量には違いが出ます。それは、被写界深度の計算で使う許容錯乱円が滅茶苦茶小さいからです。典型的には許容錯乱円のサイズは3/1000ミリメートルと大変小さい値です。
つまり、3/1000ミリメートルという小さなボケ量を前提に議論しているのが被写界深度で、この場合は焦点距離による影響は無視できるほど小さい。でも、背景ボケのような大きなボケ量の領域では、焦点距離の影響が大きくなります。
おまけ:イメージセンサーの大きさとボケ量 の関係
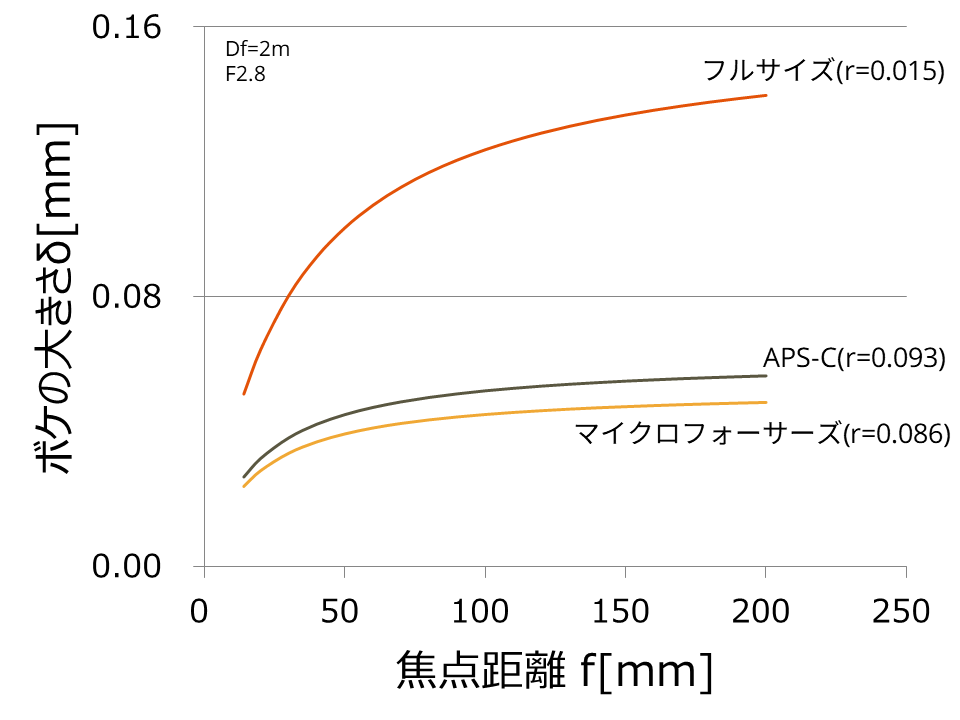
ついでに、イメージセンサーのサイズの違いがボケ量にどれくらい効くか計算しました。下のグラフを見ると、イメージセンサーが大きいほど良くボケることが分かります。意外にAPS-Cとマイクロフォーサーズの違いが少ないですね。
まとめ
レンズの焦点距離がどれくらいボケ量に効くか計算しました。被写体の写る大きさを変えない場合、望遠ほどよくボケます。また、イメージセンサー別にボケ量を比較しました。フルサイズは良くボケることが分かりました。
付録:計算方法
被写体の人間をAPS-Cの横位置で高さ一杯に写す場合、被写体の身長を160cm,APS-Cの素子サイズは23mm×15mmから、その比 r=0.0093(=15/1600)。被写体距離sは、焦点距離fを用いて次のように書けます。詳細は、別エントリ「被写界深度の不思議、望遠レンズでも被写界深度は変わらない 」をご覧ください。
また、ボケ量δと背景距離Dfは次のように書けます。ただし、FはレンズのF値。
これを式変形すると以下のようになり、上のグラフが書けます。