カメラの用語（焦点距離・ボケ・被写界深度・過焦点距離等）と原理・計算方法を徹底解説、ただし長いです。

　カメラを使っていると、様々な専門用語が出てきます。なんとなく雰囲気では分かっているつもりですが、しっくりこないので、きっちり調べてみた。それらをまとめます。

焦点距離

　光軸と平行に光をレンズに入れると一点に収束します。その収束した点とレンズの中心点（正確には主点と言う）との距離を焦点距離と呼びます。

f:id:kota2009:20171113212442p:plain

繰り出し量

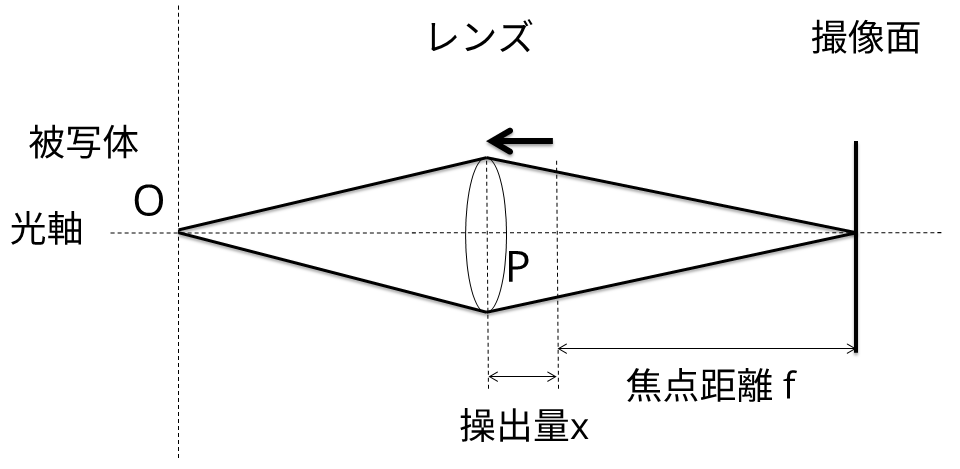
　被写体がレンズに近いとき、被写体から出た光は光軸に対して平行ではなく広がるようにレンズに入ります。すると光の収束する点はレンズより遠い側（図の右側）になります。

f:id:kota2009:20171113213125p:plain

　撮像面で光を収束させるためには、レンズを撮像面から離す（図の左側に）ように移動させる必要があります。この移動量が繰り出し量です。カメラでピントを合わせるときは、この繰り出し量を変化させています。

f:id:kota2009:20171113213842p:plain

ボケ

　上のように光が撮像面の一点に収束しているときはピントの合っている状態です。一方、被写体とレンズとの距離がずれると、そこから出る光は撮像面に一点で集まりません。ぼやーっと広がった状態になります。

f:id:kota2009:20171113212136j:plain

　撮像面を正面から見た図が下の左です。ピンボケしてボヤーっと広がった光が撮像面に現れます。この状態でシャッターを切って撮影した画像を、ディスプレイに表示すると、ディスプレイが大きい分だけ、ボヤーっと広がったボケも広がります（下図の右）。

f:id:kota2009:20171116071356p:plain

　例えば、フルサイズのカメラで撮った写真をiPhone Xのディスプレイに表示することを考えてみましょう。

　フルサイズのカメラの撮像素子サイズは36x24mm, iPhone Xのディスプレイサイズは144x71mmです。長編の長さが4倍、短辺が3倍ですので、写真は3倍に拡大されて表示されます。そして撮像素子上のボヤーとした広がりも、ディスプレイ上では3倍に広がります。

許容錯乱円

　視力1.0の人は1/60度の分解能を持っています（5m先の1.454mmを識別できる）*1。スマートフォンを30cmの距離から見るとすると、0.08724mmの分解能を持っていることになります。逆に言えば、これより小さなボケは人間の目には見わけがつきません。

　上のiPhone Xの例では、撮像素子上のボケはディスプレイ上では3倍の大きさになるのですから、逆にディスプレイ上で0.08724mmのボケは撮像素子上ではその1/3の0.02908mmのボケとなります。そして、これ以上小さなボケは人間の目には見わけがつかないことになります。

　このように人間の目では識別できない撮像素子上でのボケの大きさを、許容錯乱円と呼びます。

被写界深度

　レンズと被写体がピントぴったり位置より遠かったり近かったりしても、撮像素子上のボケが許容錯乱円よりも小さいのであれば人間の目にはピントが合っているように見えます。この距離が被写界深度です。下の図では、許容錯乱円の大きさが $\delta$ 、Df+Dnが被写界深度です。

f:id:kota2009:20171116071443p:plain

ガウスの結像公式

　ピントの合った状態で以下の式が成立します（ガウスの結像公式）。

$\displaystyle \frac{1}{s} + \frac{1}{t} = \frac{1}{f}$

　以下のその証明を示します。

　下の図は、被写体から出た光のうちレンズの光軸に平行な光線と、レンズの中心点（主点）を通る光を書いています。

　青の三角形と緑の三角形は相似ゆえ、 $\frac{s}{t}=\frac{a}{b}$ が成り立ちます。 f:id:kota2009:20171116073302p:plain

　次に下の紫の三角形とオレンジの三角形は相似ゆえ、 $\frac{f}{t-f}=\frac{a}{b}$ が成り立ちます。

f:id:kota2009:20171116074917p:plain

この二つから以下のように式変形し、ガウスの結像公式が導かれます。

$\displaystyle \frac{t-f}{f}=\frac{t}{s}$

$\displaystyle \frac{t}{f}=\frac{t}{s}+1$

$\displaystyle \frac{1}{s}+\frac{1}{t}=\frac{1}{f}$

被写界深度の計算式

f:id:kota2009:20171116071443p:plain

上の図とカウスの結像公式より以下の3式が成り立ちます。

$\displaystyle \frac{1}{s}+\frac{1}{t}=\frac{1}{f}$ $\displaystyle \frac{1}{s_n}+\frac{1}{t+\epsilon}=\frac{1}{f}$ $\displaystyle \frac{1}{s_f}+\frac{1}{t-\epsilon}=\frac{1}{f}$

一番目の式を使って( $t=\frac{sf}{s-f}$ )、2番目と3番目の式からtを消去します。

$\displaystyle \frac{1}{s_n}+\frac{1}{\frac{sf}{s-f}+\epsilon}=\frac{1}{f}$ $\displaystyle \frac{1}{s_f}+\frac{1}{\frac{sf}{s-f}-\epsilon}=\frac{1}{f}$

これらを整理すると、

$\displaystyle s_n=\frac{f\{sf+\epsilon(s-f)\}}{f^2+\epsilon(s-f)}$

$\displaystyle s_f=\frac{f\{sf-\epsilon(s-f)\}}{f^2-\epsilon(s-f)}$

これらを使ってDn,Dfを求めます。

$\displaystyle D_n=s-s_n=\frac{\epsilon(s-f)^2}{f^2+\epsilon(s-f)}$ $\displaystyle D_f=s_f-s=\frac{\epsilon(s-f)^2}{f^2-\epsilon(s-f)}$

ここでF値の定義が焦点距離をレンズ直径で割った値であることを思い出すと $\epsilon=\delta F$ であるので*2、Dn,Dfは次のように書けます。

$\displaystyle D_n=\frac{\delta F(s-f)^2}{f^2+\delta F(s-f)}$

$\displaystyle D_f=\frac{\delta F(s-f)^2}{f^2-\delta F(s-f)}$

上の式を比べると $D_f \gt D_n$ であることが分かります。つまり被写界深度は被写体の後方の方が広い（深い）のです。

過焦点距離

　遠くの物にピントを合わせると $s_n$ もレンズから離れた点に移動するのですが、無限に遠くに行くわけではありません。以下の式のように一定距離に落ち着きます。

$\displaystyle \lim_{s \to \infty} s_n = \frac{f^2}{\delta F} + f$

　上で述べたようにiPhone Xで写真を見る場合には、δは0.03 mm程度*3ですから。f=28mmのレンズを使ってF値を11まで絞ると、過焦点距離は 2.4メートル程度となります。案外レンズに近いところからピントが合うものです(iPhone Xの画面が小さいということもありますが)。

近似

　一般に s >> fが成立し（例えば、焦点距離f=28mmのレンズで被写体の距離が2m(=2000mm)など）、 $s-f\approx s$ と近似できます。これを使ってDn,Dfの近似式を導きます。

$\displaystyle D_n=\frac{\delta F(s-f)^2}{f^2+\delta F(s-f)} \approx \frac{\delta Fs^2}{f^2 + \delta Fs}$

$\displaystyle D_f=\frac{\delta F(s-f)^2}{f^2-\delta F(s-f)}\approx \frac{\delta Fs^2}{f^2 - \delta Fs}$

撮像素子サイズの異なるカメラのボケ量の比較

　マイクロフォーサーズの明るい(F値の小さい）レンズとAPS-Cの暗い(F値の大きい)レンズのどちらがボケるか気になることがあります。その比較方法を示します。

カメラ１のパラメータを以下とします。

$f_1$ ：焦点距離
$F_1$ ：F値
$L_1$ ：撮像素子のサイズ
$\delta_1$ ：撮像素子上のボケの大きさ
$\Delta_1$ ：表示ディスプレイ上のボケの大きさ

同様にカメラ２のパラメータを $f_2, F_2, L_2, \delta_2, \Delta_2$ とします。

　上のDn,Dfの近似式を式変形し、 $\delta$ について整理すると以下のように書けます。

$\displaystyle D_n=\frac{\delta Fs^2}{f^2 + \delta Fs}$

$\displaystyle \delta = \frac{D_n f^2}{F(s^2-sD_n)}$

$\displaystyle D_f= \frac{\delta Fs^2}{f^2 - \delta Fs}$

$\displaystyle \delta = \frac{D_n f^2}{F(s^2+sD_n)}$

　以後、簡単のためDnを使って議論を進めます(Dfを使っても同じ答えが導けます）。

　撮像素子上のボケの大きさと表示ディスプレイ上のボケの大きさは以下の関係で表せます。ただしQはディスプレイの大きさ。

$\displaystyle \Delta_1 = \frac{Q \delta_1}{L_1}$

$\displaystyle \Delta_2 = \frac{Q \delta_2}{L_2}$

また35mm換算で同じ焦点距離 $f_0$ (同じ画角)になるように焦点距離を選ぶとすると、35mmの撮像素子のサイズ $L_0$ を使って以下が導けます*4。

$\displaystyle f_0=\frac{L_0}{L_1}f_1=\frac{L_0}{L_2}f_2$

よって、カメラ１と同じ距離sの被写体にピントを合わせて、それよりDn近い物体のボケのディスプレイ上の大きさは以下のように書けます。

$\displaystyle \Delta_1 = \frac{Q \delta_1}{L_1}$

$\displaystyle \Delta_1 = \frac{Q}{L_1}\frac{D_n f_1^2}{F_1(s^2-sD_n)}$

$\displaystyle \Delta_1 = \frac{Qf_0D_n }{(s^2-sD_n)}\frac{f_1}{F_1}$

同様にカメラ2のボケも以下のように書けます。

$\displaystyle \Delta_2 = \frac{Qf_0D_n }{(s^2-sD_n)}\frac{f_2}{F_2}$

　つまり、 $\frac{f_1}{F_1}$ と $\frac{f_2}{F_2}$ を比較すればボケ $\Delta_1$ と $\Delta_2$ の大小を比較できます。これを使ってマイクロフォーサーズとAPS-Cのボケを比較したのが以下のエントリです。

delight.hatenablog.com

まとめ

　カメラのピント・ボケに関してまとめました。

コンパクトデジタルカメラやスマートフォンのカメラはボケにくいという理由もしっかり分かって気持ちがいい。

delight.hatenablog.com

参考文献

*1:Vol.5 視力1.0の基準はなに？ | 目のおはなし | 株式会社ニデック

*2:操出量xが焦点距離fよりも無視できるほど小さく、かつεもfよりも無視できるほど小さいとして近似。

*3:正確には0.02908mm

*4:レンズの焦点距離を35mm換算する、その理由をしっかり理解する - カメラブログ

記憶と記録

見えたことは事実ではなく自分というフィルタを通した記憶であり、さらに記憶は記録で上書きされる。写真とカメラ関係のブログです。